El Tanto Por Ciento

Porcentajes (%)

 Porcentaje quiere decir partes de un todo dividido para  100

En matemáticas, el porcentaje es una forma de expresar un número como una fracción que tiene el número 100 como denominador. 

También se le llama comúnmente tanto por ciento, donde por ciento significa 

« Un número ? de cada cien unidades». 

Se usa para definir relaciones entre dos cantidades, de forma que el tanto por ciento de una cantidad, se refiere a la parte proporcional a ese número de unidades de cada cien de esa cantidad.

Para poder resolver con facilidad ejercicios o problemas de porcentajes debemos tener presentes las siguientes medidas del porcentaje:
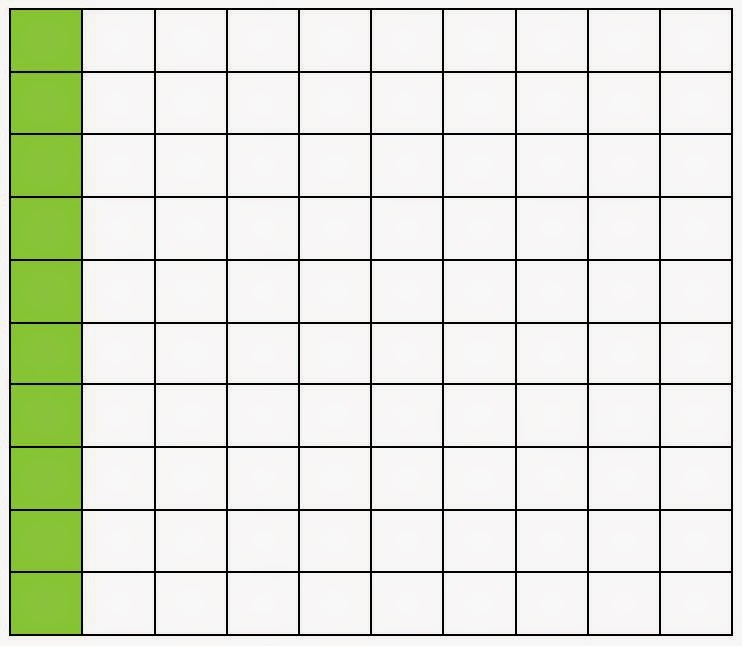
Para comprender mejor vamos a trabajar con un número. Con el 600:

100% = Es todo.

Entonces el 100% de 600 es 600

  50% = Es la mitad.

Entonces el 50% de 600 es 300

  25% = Es la mitad de la mitad o la cuarta parte.

Entonces el 25% de 600 es 150

  10% = Es la misma cantidad dividida para 10 o podemos ubicar la coma antes de la última cifra.

Entonces el 10% de 600 es 60

    5% = Es la mitad del 10% o el 50% dividido para 10

Entonces el 5% de 600 es 30

    1% = Es la misma cantidad dividida para 100 o la misma cantidad y ubicamos la como antes de la                           penúltima cifra.

Entonces el 1% de 600 es 6

Por lo tanto sabemos que cada 1% es la misma cantidad dividida para 100.
Entonces para sacar cualquier porcentaje dividimos la cantidad total o CAPITAL "C" para 100 y luego lo multiplicamos por el porcentaje o TASA "T"

También podemos aplicar la siguiente fórmula:

Sabiendo que:

C = Capital o Valor Total.

T = Es la Tasa o Porcentaje.

Si queremos sacar el 25% de 600 tendríamos que:

Observa el video para que comprendas mejor

Tips para el Porcentaje

Dale clic al enlace para poner en practica lo aprendido

Pon en Práctica lo Aprendido

Resuelve los Siguientes Ejercicios

1º De los 800 alumnos de un colegio, han ido de viaje 600. ¿Qué porcentaje de alumnos ha ido de viaje?


2º Una moto cuyo precio era de 5.000 €, cuesta en la actualidad 250 € más. ¿Cuál es el porcentaje de aumento?


3º Al adquirir un vehículo cuyo precio es de 8800 €, nos hacen un descuento del 7.5%. ¿Cuánto hay que pagar por el vehículo?


4º Al comprar un monitor que cuesta 450 € nos hacen un descuento del 8%. ¿Cuánto tenemos que pagar?


5º Se vende un artículo con una ganancia del 15% sobre el precio de costo. Si se ha comprado en 80 €. Halla el precio de venta.


6º Cuál será el precio que hemos de marcar en un artículo cuya compra ha ascendido a 180 € para ganar al venderlo el 10%.


7º ¿Qué precio de venta hemos de poner a un artículo comparado a 280 €, para perder el 12% sobre el precio de venta?



8º Se vende un objeto perdiendo el 20% sobre el precio de compra. Hallar el precio de venta del citado artículo cuyo valor de compra fue de 150 €.

75%          8140          1392          414           92           200          250          120